7.06.2021

Black holes are nature’s fastest data-scramblers, and new research suggests that secrets thrown into them may be more secure than previously thought. In a paper published in Physical Review Letters, researchers at Los Alamos National Laboratory (LANL) in the US show that once a message has been scrambled by a black hole or another system with similar properties, not even a quantum computer can put it back together.
Scramblers are quantum systems that take local information and spread it across the entire system, generating quantum entanglement between distant regions. They crop up in various contexts in physics. While black holes are perhaps the most famous example, scramblers also exist in simple systems such as spin chains – 1D arrangements of quantum particles with coupling between nearest neighbours – and in “strange” metals, in which resistivity depends atypically on temperature.
Although the scrambling process is deterministic – a fixed input yields a fixed output – scrambling systems can give rise to tremendously complex behaviour, distributing information in seemingly random fashion. This emergence of apparent randomness is known as quantum chaos, in analogy with classical chaos theory, where similarly simple systems produce equally intricate dynamics.
A shred of hope for message recovery
Physicists working at the intersection of quantum mechanics and gravity are interested in scramblers in part thanks to the so-called black hole information paradox. The paradox revolves around the ultimate fate of information that falls past the event horizon and into a black hole: after a message is scrambled across the surface of a black hole, is its information trapped in the black hole forever, or does it somehow manage to escape? One school of thought holds that information does escape from black holes in the form of photons emitted via a process known as Hawking radiation. This theory received some corroboration in 2019, but the jury is still out.
In 2007, while investigating this paradox, physicists Patrick Hayden and John Preskill came up with a thought experiment. Assuming that black holes do encode information in Hawking radiation, they showed that when a message is sent into a black hole, its pieces can be rapidly recovered by capturing a few of the emitted photons – a process akin to recovering the slices of a shredded document from the heat given off by the shredder. However, while the black hole’s scrambling behaviour makes such a recovery possible, the Hawking radiation alone doesn’t tell you how to unscramble a scrambled message. Other approaches are needed to, in effect, reassemble the shredded document from its paper strips.
Scramblers beset by barren plateaus
Enter machine learning algorithms. These powerful pattern-identifying tools “learn” how to best approximate a physical system by comparing outputs of the real system to their own outputs (given the same inputs for both), tweaking their internal model, and then rinsing and repeating until reality and approximation align. The central quantity in this learning process is a mathematical quantity known as the cost function, which captures the degree of deviation between the model and the real system.
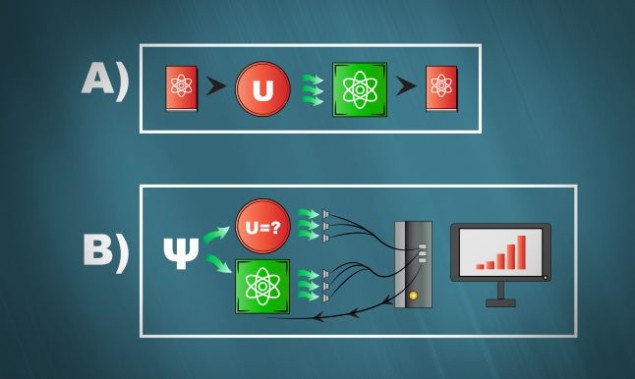
In classical machine-learning methods, the cost function is like a mountain range, replete with peaks and troughs that represent its higher and lower values. Minimizing the cost function – and learning a model for the system – is like finding a descending path and following it down to base camp. When the model is a quantum system modelled on a quantum computer, however, the cost function landscape isn’t always so rich. In fact, the LANL researchers showed that when the algorithm is asked to model a scrambler, it suffers from the problem of “barren plateaus”. “The cost function is essentially flat everywhere, with a needle-sized hole that is the base,” says Zoe Holmes, a postdoctoral scholar at LANL and lead author on the paper.
This absence of features in the cost function renders quantum machine learning ineffective, because finding the “hole” from a random starting point within the landscape is almost impossible without a downward path to follow. “If you’re learning using a cost function evaluated on a quantum computer, no matter how many training pairs you have, you won’t be able to learn the scrambler,” Holmes says, “at least without prior knowledge”. This flaw rules out the possibility of reconstructing a message, which would entail inverting the scrambling process.
A hard lesson to learn
The LANL researchers conclude that even if the pieces of a scrambled message are known, putting them back together poses a problem that quantum computers cannot help us solve. “You could perhaps (ambitiously!) try to use the fundamental physics of the black hole to put a message together,” says Holmes, cautioning that no such method is currently known, “but any learning method looks pretty doomed”. Nature, it seems, is a pretty good confidant.
Quelle: physicsworld

